Discover the card game From Zero to (super)computers!
History of Advanced Computing
Milestones in the History of Computing
1623
Wilhelm Schickard invents the first mechanical calculator, the Speeding Clock, which allowed the user to add and subtract numbers up to six digit numbers. He wrote to the astronomer Johannes Kepler to explain to him how to use the machine in order to calculate the ephemerides, i.e. the position of the planets as time advanced. The Speeding Clock was destroyed in a fire before being completed.

Wilhelm Schickard, inventor of the first mechanical calculator.
1645
Blaise Pascal carries out the first computations on the Pascaline, the world's first operational mechanical calculator. It was able to add and subtract (though this operation was rather difficult to implement) and in 1649 Pascal was given a royal monopoly on the sale of his machines in France. Three years later he had sold a dozen of his calculators. Due to his role an important computer language of the 1980s was named Pascal.

The Pascaline
1672
Gottfried Wilhelm Leibniz constructs the Stepped Reckoner, the first calculator able to carry out all four basic arithmetic operations (addition, subtraction, multiplication and division). Only two examples of this machine were ever built. Leibiz also deserves credit as the inventor of the system of binary (base two) arithmetic that is used in all modern computers.

The Stepped Reckoner
1820
Thomas de Colmar builds his first Arithomètre, which was the first reliable calculator to be mass-produced. More than 5000 were constructed, up until the beginning of the First World War (1914-1918).

The Arithomètre
1822
Charles Babbage develops the theoretical concept of a programmable computer. This computer would be designed to replace the calculations done by humans, subject to frequent errors. Babbage's "analytical engine" had very similar architecture to that of modern computers, with distinct memory zones for the data and the program, the existence of conditional jumps as well as a separate unit for handling input and output.
This concept was described in detail by Ada Byron, Countess of Lovelace(daughter of the famous Romantic poet Lord Byron). She is also credited with having written the first computer program (to calculate a sequence of Bernoulli numbers), though historians are not in agreement over the relative importance of Ada Byron and Charles Babbage in the development of this program. In 1980, the American Department of Defense named the language it had developed "Ada" in her honor.

Ada Byron, Countess of Lovelace
1854
The English mathematician George Boole published the book Laws of Thought which lays the mathematical foundations for binary arithmetic and symbol logic (using the logical operators AND, OR and NOT), ideas that were of fundamental importance in the construction of 20th century computers.

George Boole
1890
Herman Hollerith constructs a machine which can read perforated cards and then carry out statistical calculations based on the data read from these cards. The first system of this kind was ordered by the Census Bureau of the USA. A few years later Hollerith founded the Computing Tabulating Record, which became IBM (International Business Machines) in 1924.

A Hollerith keyboard (pantograph) punch
1936
Alan Turing develops the concept of the Turing Machine, a purely theoretical device able to manipulate abstract symbols and which captures the logical processes of any possible computer. This machine in fact is a Gedanken experiment, which allowed Turing and later computer scientists to better understand the nature of logic and the limits of numerical computation, resulting in the detailed formulation of such concepts as algorithms and computability.

Alan Turing
1939
Bell Laboratories in New Jersey complete the CNC (Complex Number Calculator), an analog computer based on electromagnetic relay switches. In 1940 its inventor, George Stibitz used this computer, installed in New York, from his office at Dartmouth College in New Hampshire, thereby establishing the first use of a computer by network.

The CNC (Complex Number Calculator)
Early Computers
1941
Konrad Zuse finishes the construction of his Z3 computer in Germany. It's the first completely automatic and programmable calculating machine in history. The Z3 consisted of 2000 switches, with a clock frequency of 5 to 10 Hz and a word length of 22 bits for binary computations, or around seven significant digits. An addition took on average 0.7 seconds, a multiplication 3.0 seconds. The Z3 consumed 4 kW of electricity and was destroyed during an Allied air raid in 1943.
1942
The Atanasoff-Berry Computer (ABC), named after its two designers, is completed at Iowa State College. It's the first digital computer, containing 280 vacuum tubes and 31 thyratons. Designed to solve a system of 29 linear equations, it's nonetheless also programmable. Though the computer was never entirely functional, it was a source of inspiration for the design of ENIAC.

The Atanasoff-Berry Computer (ABC)
1943
The Colossus computer is developed in Great Britain to aid in the decryption of coded German messages. It's the first programmable electronic computer, in which the program was altered by reorganizing its cable network. Like the ABC, it used vacuum tubes but also photo-multipliers which allowed to read in paper tapes containing the German ciphertext.

Construction of the Colossus
1944
IBM delivers the Mark I to Harvard. This computer consisted of 3500 switches and around 500 miles of wiring. It was able to carry out calculations with 23 significant digits, with an addition or subtraction requiring 0.3 seconds and a multiplication 6.0 seconds. The Mark I was able to read instructions from a tape of perforated paper in a sequential manner; thus it was possible to create a program loop simply by reinserting the tape back into the reader.
One of the first individuals to have used this computer was Rear-Admiral Grace Hopper. She developed the first compiler for a computer language (called "A") at the end of the 1950s. She is also credited with having invented the word "bug" because of the following anecdote: a technician working on the Mark II (successor to the Mark I) found a moth in one of the switches, thereby disabling it. Hopper glued the insect in her journal and wrote the caption, "First actual case of a bug being found". Nevertheless, the term bug was already frequently used at this time to describe technical problems.

Rear-Admiral Grace Hopper
1944
The Electronic Numerical Integrator And Computer (ENIAC) is built at the University of Pennsylvania. It was the first general purpose electronic computer with only one example ever being built. It was ordered by the US army in order to calculate ballistic tables for the artillery and it cost approximately $500,000 to build. ENIAC consisted of 17,500 vacuum tubes, 1,500 switches and weighed 27 tons; its electricity consumption was 150 kW. It also possessed an input device capable of reading perforated IBM cards. Doing base 10 calculations with 20 significant digits, it was able to perform 5000 additions or 385 multiplications a second, a very important improvement compared to earlier computers.

The Electronic Numerical Integrator And Computer (ENIAC)
1947
William Shockley, Walter Brattain and John Bardeen successfully test the contact transistor, which was the basis for the semi-conductor revolution. Bell Labs later improved the concept which, being smaller, more reliable and consuming less energy, rapidly replaced the older vacuum tube technology used for building electronic computers.

Bardeen, Shockley et Brattain in 1948
1959
Jack St. Clair Kilby, working at Texas Instruments, creates the first integrated circuit (i.e. an electric circuit consisting of transistors, resistors and capacitors built on a single semi-conductor substrate) using a germanium base.
1961
Robert Noyce, at Fairchild Semiconductors, builds an integrated circuit using a silicon base, which will be the first commercial integrated circuit.
1971
Ted Hoff and Federico Faggin at Intel, in collaboration with Masatoshi Shima at Busicom, design the first commercial microprocessor (i.e. an integrated circuit corresponding to an entire central processing unit (CPU)), the Intel 4004, with a clock speed of 740 kHz, allowing it to carry out 92,000 instructions per second (it's important to note that an addition involves several instructions - the number of instructions required depends on the processor). Just one of these processors, a few centimeters long, has the same computational power as ENIAC.

The Intel 4004 microprocessor
Fin des années
1970
The first personal computers begin to appear: the Commodore PET, the Atari 400 and 800, the Apple II and the TRS-80. In 1981 IBM begins constructing its IBM 5150, marketed as the IBM PC. The huge commercial success of this computer created a de facto standard and several companies employed the architecture of the IBM PC in designing their own machines. This was made possible by the fact that IBM had decided to make the PC's system architecture public in order to favor the growth of competition in the market for PC components.

The Commodore PET
Supercomputers
1961
IBM builds what can be considered the first supercomputer, the IBM 7030, also called "Stretch", which was delivered to the research laboratories at Los Alamos. Sold for $7.78 million, this computer was the most powerful in the world until 1964.

The IBM 7030
1964
Seymour Cray, then an employee of Control Data Corporation, was the chief designer of the CDC-6600, a computer three times more powerful than the IBM 7030. Several versions of the CDC-6600 were created, one of which had a dual core CPU. It was also the first computer to carry out calculations in parallel and possessed:
• 128 KB of memory;
• a clock speed of 10 MHz;
• a peak performance of up to 3 MFLOPS.
The successor to this machine, the CDC-7600, possessed an architecture that prefigured the vector processors used in later generations of supercomputers.
1972
Seymour Cray founds Cray Research Inc., the company which will dominate the supercomputer industry until the end of the 1980s. Its first product, the Cray-1, was a vector computer that became in its subsequent implementations the first shared memory computer (Steve Chen). This computer contained around 200,000 logic gates, approximately the same number as could be found in the Intel 80386 processor (introduced in 1986).
Two characteristics contributed to the success of this computer. Firstly, it had a vector processor that allowed loops of instructions to be executed in a pipeline fashion much like an assembly line at a factory, dramatically increasing the speed of execution. The Cray-1 also had registers, ultra-rapid memory units, which could be used to eliminate a bottleneck in numerical computations. Registers are now present in all computers, with only the size varying from one system to the next!
The first Cray-1 was delivered in 1976 to the Los Alamos National Laboratory in New Mexico. The second was purchased by the National Center for Atmospheric Research (in Colorado) in 1977, for $8.86 million.

The Cray-1
1982
The Cray X-MP succeeds the Cray-1. This is the first parallel computer. It reached a performance of 800 MFLOPS and will be followed in 1985 by the Cray-2, whose performance could achieve 1.9 GFLOPS.
1986
Apple buys a Cray X-MP in order to design its new Macintosh, causing Seymour Cray to observe,"This is very interesting because I am using an Apple Macintosh to design the Cray-2 supercomputer".
Fin
1980
Massively parallel computers become more common and eventually occupying pride of place in the world of supercomputers. Their basic principle consists in dividing the computational load among many processors (individually less powerful than those in a Cray), each of which has its own memory and computing capacity. Among the machines, which see the light of day are Thinking Machines' Connection Machine, Kendall Square Research's KSR1 and KSR2 and shared memory systems like nCUBE's eponymous system and the Meiko Computing Surface from Meiko Scientific.
• The CM-1 contained up to 65,536 (216) processors, each possessing 512 bytes of memory; to read an interesting article on Richard Feynman's role in this adventure, Click here.
• The KSR1 contained up to 1088 (17*26) processors in a shared memory configuration, each processor having a clock speed of 20 MHz and a peak performance of 40 MFLOPS.
• The nCUBE (1985) contained up to 1024 (210) processors, each processor possessing 128 KB of memory and a peak performance of 500 KFLOPS. Up to eight terminals could access the computer at the same time.
The most widely used operating systems of the era are Unix and VMS.

A CM-2 by Thinking Machines (1987)
1993
Cray having noted the efficiency of parallel computation joins in the new direction by using the fastest processor of the day, the DEC Alpha 21064, with a clock speed of 150 MHz; it begins selling the T3D, a computer with up to 2048 (211) processors and becomes once again a leader in the field of supercomputing.

A Cray T3D
Années
2000
A new evolution takes place in the world of supercomputing - rather than use architectures specifically designed for scientific computation, manufacturers choose to employ standard commodity parts (memory, CPUs, disks and network interfaces) to build clusters of PCs, connected using a network.
Equations in Physics
Since the existence of the first civilizations (and perhaps before, though we’ve no written record) human beings have sought to understand the basic rules of Nature.
In ancient Greece, when such rules were discovered, they were expressed using words which allowed them to be described. The resulting expression could be difficult to comprehend as can be seen with the following extract from the Complete Works of Archimedes, discussing what happens when a body is submerged in water.
These lines express the concept that we now know as Archimedes’ Principle and which can be written mathematically in the following manner:
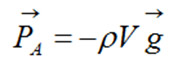

Archimède
This equation tells us that a body submerged in water will be subject to a force PA which is proportional to the density ρ and the volume V of the fluid displaced and pointing in the opposite direction of the local gravitational force g. This single equation allows us not only to understand that only part of an iceberg appears above the water’s surface because it is less dense, but also to calculate what percentage is visible using the ratio of the water’s density and that of ice. Thus a few symbols are sufficient to replace an entire page and a half of explanatory text and this is precisely the value of mathematics in science – it allows us to express complicated ideas in a precise and compact manner.
You may wonder why Archimède chose not to employ this formulation to describe his observations since the Greeks knew how to calculate! In fact, even before the Greeks, Mesopotamians and Egyptians had some understanding of geometry and algebra. Nonetheless, just as we learn when we’re young not to add apples and oranges, at that time no one had had the idea to multiply quantities which expressed different concepts. If for example it was possible to multiply a length by another length to obtain an area, no one would have dared to imagine dividing a mass by a volume to obtain a density! As well, mathematics was itself for centuries expressed in the form of words rather than the compact symbolism with which we’re familiar today.
It was during the Renaissance that equations, similar to those we know today, began to appear. First, Europeans had to become aware of Arabic and Indian mathematical writings and give up Roman numerals in favour of the Arabo-Indian notation, as well as adopting the concept of zero. It was also at this time that mathematical symbols first appeared, for example Nicole d’Oresme employed the + sign around 1360 while, in 1557, Robert Recorde introduced the = sign to represent equality.

Galilée
In the same period, Galilée (1564-1642) laid the foundations of the scientific method, based on the comparison of experiment and theory. To do this, he made use of a precise mathematical description of the phenomena that he studied, constituting thereby one of the first unions of physics and mathematics. He wrote:
“Philosophy [i.e. physics] is written in this grand book – I mean the universe – which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering around in a dark labyrinth.”

René Descartes
Descartes (1596-1650) carried out the next step, with the development of analytic geometry. This branch of mathematics is based on using the principles of algebra to study geometry, thereby associating numerical values (the coordinates) and graphical representations.


