Brain Mapping

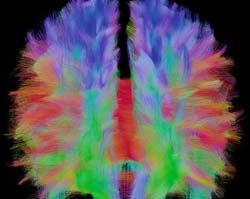
Connectome of a human brain

With Maxime Descoteaux, white matter takes on the colors of the rainbow and the brain becomes a sophisticated tangle of nerve fibers. He is the image wizard who reads in the diffusion of water to reveal the paths of our intellect, the mathematician who puts the pedal to the floor on the brain’s highways.

Why Visualize White Matter?

Image processing techniques have helped tremendously the medical field to better diagnose dysfunctions of the human body. All kinds of signals, such as ultrasound, X-rays, etc., are now used to construct images of what is invisible to the naked eye. It is so for what lies in our skull that is revealed mainly with the technique of magnetic resonance imaging (MRI).

MRI acquires magnetic signals produced by the hydrogen atoms of the water found in the nervous tissue. From this technique was developed diffusion MRI (dMRI) which measures the diffusion of water molecules in different directions. Since the movement of water molecules is constrained by the structure of the tissue, dMRI allows us to view nerve fibers. Until recently, this test took a lot of time. Now, thanks to mathematical tricks, Maxime Descoteaux accelerated the speed of images processing to only 10-20 minutes without losing quality.

The brain consists of gray matter, composed of neuronal cell bodies, and of white matter, composed of axons of neurons also called fibers. The signals generated in the cell body spread in the axon to the nerve endings where they are transmitted to other neurons. The fibers are therefore similar to the cables connecting the various regions of the brain and allow neurons to communicate with each other. It is thus necessary to examine the interconnections between nerve centers to elucidation brain function.

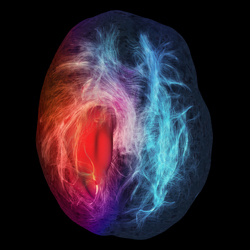
Fibers in a tumor

dMRI is a noninvasive technique, it can be used safely to study the development of the architecture of the brain from birth to adulthood. It can also detect when the communication pathways are damaged, which is an indication of several neurodegenerative diseases such as multiple sclerosis, Alzheimer’s or Parkinson’s disease. Finally, it can help physicians make a preoperative assessment of brain tumors and more accurate surgery. Indeed, a tumor can block the passage of fibers, bifurcate them or new connections can reshape itself around the mass. Better three-dimensional visualization of all these connections allows identification of the affected areas to avoid sacrificing viable neurons during surgery. So we can say that the work of Maxime Descoteaux helped bridge the gap between mathematical research and computer imaging techniques and their application in the biomedical discipline in a clinic level. Today, experts from around the world use the method in hospitals.

How to Handle Data

The work of Maxime Descoteaux’s research team consists in virtual reconstruction of nerve fibers in 3D. First, in each 2 mm cube of the brain (voxel) the signal measured by the dIMR is used to calculate the intensity of the diffusion of water molecules in various directions. Then, for each voxel, one estimates the main direction of water diffusion, which would correspond most to the orientation of the nerve fibers contained in the voxel.

The two main methods used for this purpose are the diffusion tensor imaging and high angular resolution diffusion imaging (HARDI). The problem with diffusion tensors is that they assume a single bundle of fibers through a voxel while in fact each can contain half a million fibers intersecting. HARDI methods in turn, allow the reconstruction of intersections of fibers within a voxel, but require the measurement of more than 30 directions, which extend substantially acquisition time of the signals. Fortunately, the choice of a clever sampling strategy can alleviate this problem. Thus, instead of sampling the integrity of the voxel in a Cartesian grid of 500 points, one can measure fifty points on the surface of spheres fitted into each other. This analytical reconstruction represents many advantages. It is up to 15 times faster, improves the angular resolution of more than 15 times and minimizes the effects caused by noise.

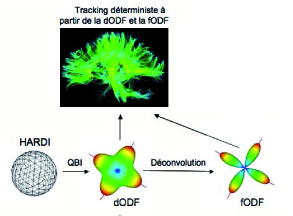Maxime Descoteaux proposes to apply this method of spherical deconvolution to the signals of water diffusion to obtain an estimate of the fiber orientation distribution function (fODF). From the angular information of these local estimates, tractography algorithms produce 3D curves connecting two voxels. Deterministic tractography method based on the use of the maximum fODF, is thus an easy and effective way to get an idea of the fiber pathways with only a few points. Crossing fibers are found in places with several maxima that lead the track to divide. Maxime Descoteaux’s team concluded therefore that the fODF greatly improves the results of tractography in regions with complex branching fiber bundles.

Until recently, looking at the map of neural pathways plying our brains, we could only see the major highways linking brain areas, but not the small side roads that intersect. Now, thanks to the spherical deconvolution and tractography algorithms developed by Maxime Descoteaux, there is a better and faster visual representation of the white matter of the brain. This growing knowledge about connectivity will undoubtedly help to elucidate the harmony of this neural network that is our brain.